The Relativistic Electron Before Relativity

Dealing with Relativistic Results 1899-1905

This set of posts from five years ago is about the problems of moving a relativistic object in the Undetectable Aether when you have problematic experimental data to deal with as well. Remember also that Larmor had shown by 1900 that if the aether could be detected, that is if the motion of the Earth through the aether had electromagnetic effects, then it could be used as an endless source of infinite power forever. Not only did this seem somehow unlikely, but not the least whiff of the aether had ever been reliably detected. So the aether had to act on electrons in an undetectable way, maybe by squeezing them somehow in some alternative set of coordinate systems. Einstein was able to resolve all of this in 1905 and his relativistic (special relativistic) solution was accepted by cutting-edge physicists (such as Plank, Sommerfeld and Minkowski) within a few years.

Still, in the years before relativity, things were very confusing. For the Lorentzian (and Larmorian) theories of the electron, matter, optics, the aether and the electromagnetic fields to interact as required, the aether had to be undetectable and this involved multiple coordinate systems and different ways of deforming the electron. As we have seen (in the post “Reality Dragged from the Aether”), Larmor worked these requirements out independently by 1900 while these requirements only became clear to Lorentz in 1904 after elaborating his theory of the electron in the context of Kaufmann’s experiments and Abraham’s explanations of them.

Basically, for Larmor and Lorentz, the aether had to be undetectable because Lorentz invariance (and the associated “contraction” of matter) concealed it. Much to Abraham’s horror, this concealed action of the aether meant that there were forces in the universe other than electromagnetism and the entire thrust of physics in 1903 was to set aside the discredited mechanical world view and build up a picture of the universe based purely on electromagnetism. As Janssen and Mecklenberg point out in their “Electromagnetic Models of the Electron and the Transition from Classical to Relativistic Mechanics”:

A choice had to be made between the objectives of Lorentz and Abraham. One could not eliminate all signs of the Earth’s motion through the aether and reduce all physics to electrodynamics at the same time. Special Relativity was initially conflated with Lorentz’s theory because it too seemed to focus on the undetectability of motion at the expense of electromagnetic purity.

But when Kaufmann began his series of experiments in 1901 to determine the effect of an electron’s velocity on its mass, the need for such a choice was not yet part of the theoretical problems of the electron. Miller points out that Kaufmann was following up on Wilhelm Wien’s 1900 outline of a research program to build an alternative to Hertz’s 1894 proposal to develop a completely mechanical description of the universe, which had not proved fruitful. Wien thought experiments to resolve the increasing mass of the electron as the electron’s velocity increased to one third the speed of light as presented in Lenard’s work with cathode rays was the place to begin building an electromagnetic picture of how the universe was constructed. (see A. I. Miller, Albert Einstein’s Special Theory of Relativity. Pages 46 and 47). Lorentz in 1901 was not so sure about how to deal with the relation of an electron’s “real” mass (“mechanical” = “real” at this point for Lorentz) to its “apparent” (or “electromagnetic”) mass.

Kaufmann, on the other hand, thought it could all be clarified with his experimental work thus pushing aside the “sterile,” mechanical imagery of the world and beginning anew with the electron as the primordial building-block of the universe. Rather than being sterile, the electron was stunningly fecund; it appeared to explain luminous vapors, the Zeeman Effect, Planck’s constant, stellar aberration, electrolysis, the photoelectric effect and radioactive decay. It’s strange that Kaufmann doesn’t seem to have mentioned X-rays, but since he was going to be using beta-rays (electrons) from radium decay in his experiments maybe adding X-rays to the list might have seemed excessive and, of course, in 1901 the nature of X-rays was still not clear except for the general notion that they were not electrons.

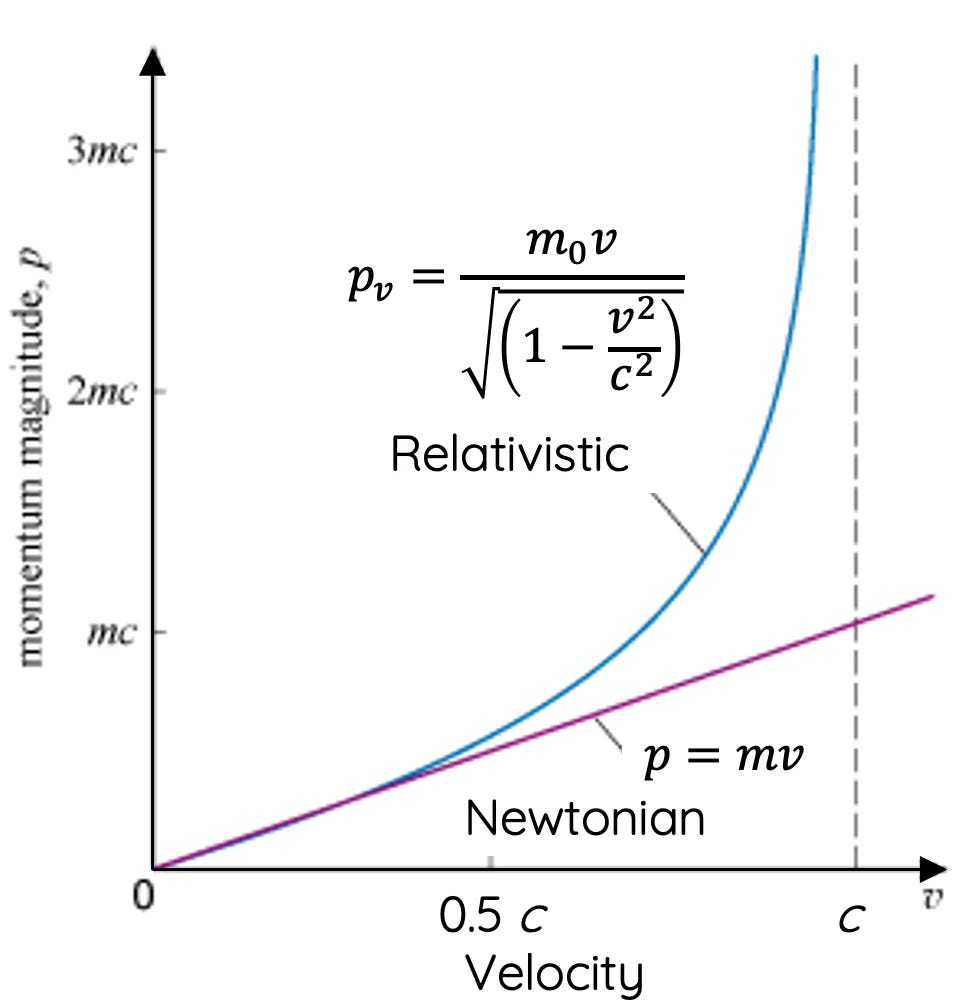
As Miller sets the stage on page 48 of Albert Einstein’s Special Theory of Relativity, Kaufmann wanted to use beta-rays since they went up to three times faster than cathode rays (ie the electrons of cathode rays were measured traveling at speeds up to 0.3c, about one third the speed of light while beta-ray electrons had been measured at speeds of up to 0.9c). In 1899, William Sutherland put that close-to-light-speediness in the context of the concerns of the time, pointing out, “The electrons stream through the aether with nearly the velocity of light and yet provoke no noticeable resistance. What wonder, then, that any aethereal resistance to planetary motion has remained beyond our ken!” At such high speeds, the additional mass that the electrons acquired due to their velocities would be open to exact measurement by tracing the effects on their trajectories by using electrical and magnetic fields of known strength. For cathode rays these kinds of measurements had determined the ratio (at least) of the electron’s charge to its mass. But what if the field of the charge, interacting with other fields, determined the mass? Miller notes that J. J. Thomson had worked out this possibility as early as 1881, work that was clarified by Thomson and Heaviside in 1889 and Searle in 1897. Kaufmann used Searle’s expression for the mass increase caused by the movement of a spherical body with a uniform surface charge distribution as his basic phenomenological reference point in describing the meaning of the curves that his beta-rays (presumed to be spherical electrons) produced on photographic emulsions after passing through a set of parallel fields.

Miller says (page 54) that in the process of making sense of Kaufmann’s data: “…on 11 January 1902, Kaufmann’s colleague at Goettingen, Max Abraham, proposed the first field-theoretical description of an elementary particle.” Abraham revised the mass calculation implied by Searle’s work and noted a little later in 1902 that, given his description of the electron, “however continuously the aether manages to fill space, electricity has an atomistic structure.”

From there on into the interior of Abraham’s electron, things get very strange even in Miller’s lucid account. If I understand correctly what is going on with what Abraham called “the Lorentz-Poincaré equation,” Lorentz and Poincaré had proposed a formal function G of the aether to account for all the energy involved in moving electrons. For them, it was a sort of theoretical book-keeping function to sustain the conservation of energy over all of space and time. Abraham used this same function, calling it the “electromagnetic momentum density,” G, but took it to be a real and direct impact within the aether in the present set of local time frames (ie not in a theoretically infinite time) caused by moving electrons.

It might be worth noting that some of these early approaches to the electron suggest some of the methods that eventually were used later in the century to account for events surrounding electrons and energy (e.g. “the Dirac little delta function” that touches briefly at infinity as a normalizing distribution), but the whole range of the electron’s energy states are very hard to describe without special relativity and the kind of transformations and virtual interactions suggested in the quantum electrodynamics of the later 1940s. Larmor, Abraham, Lorentz, Kaufmann and Poincaré had run into a set of interrelated problems, such as what would later be described as virtual particles and the self-energy of the electron, that were impossible to unravel without special relativity and some kind of quantum approach. Moreover, many components of their world-picture (or as Janssen and Mecklenberg put it, their dreams) – the electron as a fundamental building block involved in all forces, the aether, local versus universal time and so on – were more hinderances than helpful things.

Speaking of unraveling, at this point in the parallel explanations of Abraham’s theory of the electron, Janssen and Mecklenberg have an enormous footnote which we will use to escape from this post with some cliff-hanging conclusions. First, you can see Lorentz’s contraction and aethereal book-keeping as a set of methods for keeping the aether out of local expressions of electron energy. Second and similarly, you can see Abraham’s use of electromagnetic momentum that includes the aether as a way of shrinking the effects of the aether into the electron. In both cases the effects of the aether are removed from descriptions of the electron, though with odd and specific effects on the surface dynamics of the electron itself – ie. The Lorentz electron deforms and the Abrahamic electron has some problems dealing with its momentum (ie the electromagnetic momentum is not the only momentum involved in the electron’s movement). The cliff-hanger is that Planck, Ehrenfest and Einstein worked this out in 1907 as we will see and there is even another loose end involving what is sometimes called Poincaré Pressure and three letters that Miller discovered at the Algemeen Rijksarchief, The Hague, in the early 1970

It’s hard not to draw some overall and highly anticipatory conclusions from looking at how the activity of picturing events surrounding the electron as an elementary particle evolved quite rapidly. One thing that stands out for me is not so much the evolving imagery of theory and experiment but rather the growing acceptance that some things about elementary interactions cannot be usefully fully pictured from certain points of view. One sees physicists learning to accept that from some levels of analysis the phenomenological or even full theoretical descriptions do not show every phase of an event as a simple image. In only a few years after 1904 it is shown that moving reference frames don’t even necessarily show events in the same sequence and that the shape of the electron has no significance and that the book-keeping function of overall energy in an aether-filled universe has no impact on events at the level of electron interactions. This growing acceptance of levels of approximation even for seemingly simple events is a theme that intrigues me and I think it is a theme that is both useful in terms of understanding how people made sense of what they were seeing in experiments while at the same time being something that is such a basic assumption now that it is more or less invisible as a development over time. It is too obvious to see as something that had to be accepted slowly. Moreover, some of the attempts to explain this obvious-but-hard-to-specify aspect of how physics works out pictures of the world can end up being quite confusing – though I hope not to go into that at the moment. As usual, we will attempt to dwell in the confusion for a while.

Another retrospective theme in addition to that of foreseeing developmental trends is “acceptance” – ie. The question of how theorists came to discard their earlier views. In this period, as we will see especially with Richardson, Compton and Anderson, experimentalists did not pay much critical attention to theoretical developments. As an experimentalist, Kaufmann was something of a brave exception. Here, I think we find some other surprises. For example, Planck had no trouble finding himself at home very early on in Special Relativity, while having a lot of trouble (as did Bohr) accepting the light quantum as a real dynamic object. Pais remarks in Inward Bound, on the basis of his conversations with Einstein, that the “revolutionary” moment that Bohr and Einstein (and Schrödinger obviously) could not quite get over was Born’s probability interpretation of the wave function. So different physicists had very different sets of theories they could accept. Some physicists, such as Born, Sommerfeld and Hans Bethe simply went along working out what they could and not worrying much about accepting or discarding theories as they went from problem to problem.

Still, whatever my second thoughts about how not to keep getting ahead of the story, Lorentz’s electron from 1904 is next on the chronological agenda. In the early 1970s Miller wrote (first essay in Frontiers of Physics: 1900–1911):

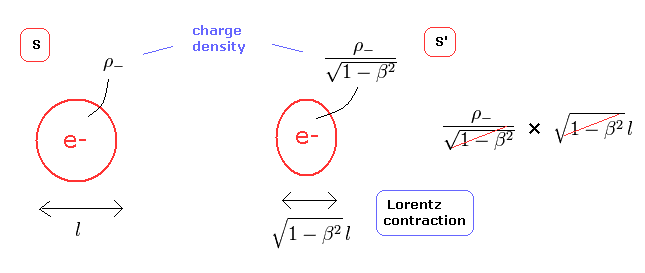
[In 1904], based on Kaufmann’s data, the new second-order aether-drift experiments of Trouton and Noble [which were noted here in “Reality Dragged from the Aether”], and those of Rayleigh and Brace, Lorentz extended his electromagnetic theory to a theory of the electron. Whereas Abraham’s electron was a rigid sphere, Lorentz’s was deformable and he postulated that when at rest it was a sphere, but it contracted when moving…. Then, using the same approximation as Abraham, Lorentz derived transverse and longitudinal masses for his electron.

Lorentz showed that his masses, also agreed with Kaufmann’s data. This time Poincaré found no faults with the foundations of Lorentz’s theory, but he quickly caught several technical errors, and his keen sense of aesthetics revealed to him certain symmetries that Lorentz’s original mathematical formulation had obscured. Poincaré’s completed work appeared in his classic paper of 1906, “On the Dynamics of the Electron”; a short version of this paper had appeared in June 1905.The development of certain key results that survived the eventual demise of Lorentz’s theory of the electron are in three letters that Poincaré wrote to Lorentz, which I discovered at the Algemeen Rijksarchief, The Hague.

So the mysterious three letters! More to the point, as Miller describes Lorentz’s theory of the electron, it uses a lot of coordinate systems starting with an auxiliary system X’ in which the Maxwell–Lorentz equations have the same form as they do relative to an ether-fixed reference system; the coordinates (x, y, z, t) refer to an inertial reference System S prime; and x, = x – vt, y, = y, z, = z, t, = t, where (x, y, z, t) refer to the ether-fixed system X. Lorentz’s goal was to transform the fundamental equations of his electromagnetic theory from the inertial system S prime to the fictitious reference system X” in which he could perform any necessary calculations, and then transform back to S. For example, it was particularly useful to take X” to be the electron’s instantaneous rest system in order to reduce problems of the electrodynamics and optics of moving bodies to problems concerning bodies at rest. In summary, there were three reference systems in Lorentz’s theory — S, S prime, X’ – the aether-fixed auxiliary system possessing no physical interpretation. Consequently, there were two sorts of electrons: the “real” electron of the reference systems S and S prime, and the “imaginary” electron in X’. Taking X” to be the electron’s instantaneous rest system meant that in order for any other system to have the same properties as the ether-fixed system, the imaginary electron had to be a sphere in X” in imaginary fixity. But from the spatial portion of the Lorentz transformations the electron in X” is deformed. Therefore in order to maintain the theorem of corresponding states, the moving electron in S, must be deformed in a manner that compensates for the deformation in X’.

Miller’s explanation continues:

Lorentz’s supporting argument for this postulate of deformation included inverting the spatial part of the Lorentz transformations. In order to render the postulate of contraction further “plausible,” to use Abraham’s word from his subsequent criticism of Lorentz’s theory of the electron, Lorentz proposed further interlocking postulates; among them was a postulate that the as yet unknown intermolecular forces transformed like the electromagnetic force in order that macroscopic matter contracted when in motion. Thus, to Lorentz and Poincaré, covariance was a mathematical property that was achieved through postulated transformations, which did not possess an unambiguous physical interpretation, because the transformations contained unknown velocities relative to the ether. The reason is that in electrodynamics and optics of 1905 [ie before special relativity], the ether-fixed reference system S was cavalierly taken to be the laboratory system. The tacit assumption was that the ratio of the laboratory’s velocity relative to the ether with that of light was small enough to be neglected. In other words, the notion of at rest relative to the laboratory was not well defined.

Oddly enough, this all worked better in phenomenological/experimental terms than Abraham’s theory did, for while it was a tight squeeze to get better agreement between Abraham’s theory and Kaufmann’s results, Abraham’s theory predicted a double refraction that no one observed. Lorentz’s “as yet unknown intermolecular forces” acted (theoretically) to prevent that unobserved phenomenon. In this respect Lorentz’s theory strongly resembled Larmor’s aether-based theory from 1900.

Even more oddly, as Miller describes things on page 78, the complete energy of the electron has some twists in its calculation in the two different theories. In Abraham’s, the electron undergoes an imaginary contraction in an imaginary coordinate system, while in Lorentz’s theory, the electron really contracts in the direction of the motion but remains a perfect sphere in the related imaginary coordinate system.